如何设计一个平衡树结构

(感谢”杀出一条蟹路“同学帮忙复核数学推理)

昨天在群里和一些同学讨论算法，扯到平衡树。突然想写点东西，给同学们分享分享。但是我今天要分享的不是有多少种平衡树实现，而是如何设计一种平衡树。

希望通过这个分享，能让同学们有一些基础的认识，一种数据结构/算法是如何设计出来的。

而我们今天的话题，就是如何在树节点上，通过附加一个size来进行树平衡。

0. 开始之前

当我写这篇文章的时候，我希望对算法有所了解的同学都能看懂。数据结构设计相对于算法来说，还是有那么一点点的偏难。有些概念可能大家都是第一次接触，因此我在这里先进行一些基础概念的讲解。

约束

数据结构设计和一般性的算法有一个非常大的差异，就是：

数据结构是一个在一段时间内存在，并持续维护的结构。而不是一次性运行结束的函数调用。

这中间的最大差异是，假设我们现在定义一棵树是平衡的，那么树的高度$H < 2 log_2(n+1)$。假设我们这时需要实现一个函数isBalanceTree(root)，那么显然除了完整的遍历整棵外，我们并没有其他什么办法。显然这个时间复杂度是O(n)的。

判断一个树是否是平衡的，这个都是O(n)的了，如果我们需要写一个函数balanceTree去平衡一棵树，这个时间复杂度至少是O(n)。

如果说我们写一棵普通的二叉树，然后每次插入/删除后，我们运行一次balanceTree我们也可以得到一棵平衡树。但是这个明显没有多大意义。还不如弄个数组，每次先定位再插入，不但简单，还来的快。

那我们如何来解决这个问题，中间的“秘密”就是约束。

所谓约束就是：数据结构在“平时”应该满足什么限制。

如果说一个数据结构，只要满足了某约束，就能带来某个我们想要的特性。而我们每次修改数据结构时，只需要很小的代价，就能保持这个约束。那么这就是我们想要的。

当然，上面的讲的太抽象了，这里我们拿个红黑树举例。

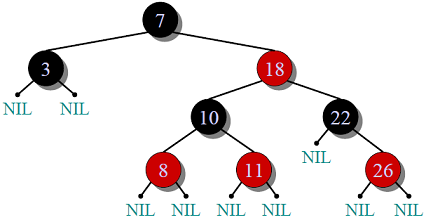
红黑树在二叉树的基础上，引入了4条约束。

1. 节点必须是红色或者黑色
2. 根节点是黑色
3. 红色节点不能和红色节点相邻
4. 从根节点出发，到任意nil节点所路过的黑节点数量一致

假如说我们记从根节点出发，黑色节点数为d，树的最大高度为h。

从约束4我们知道，d对于任意路径都一样。

从约束1和3我们知道，$h \le 2d$。

另外我们知道，对于任意红黑树，$总节点数n \ge 黑节点数 \ge 2^d-1$

于是，我们知道：$h \le 2d \le 2log_2(n+1)$

因此，我们从红黑树的约定中，我们推出了我们想要的平衡。

另外，红黑树对于插入/删除时，有一套完整的修正约束的方法，这里我们就不展开讲了，有兴趣的同学戳这里：维基百科-红黑树

注：上面的分析中，我们并没有用到约束2，约束2不是可选的，是红黑树上升的重要约束。

分析

接着我们需要一个合适的衡量指标去衡量我们的目标是否达成。就像是我上面举的定义，稍作放松是完全可以用的。但是这里我还是想探讨一下如何定义一个良好的衡量，用作后续的分析。

显然，“平衡树”是一棵树哈。我们这里更关心的是“平衡”。所谓的“平衡”就是：树中间的最深叶子节点的深度和最浅叶子节点的深度差的“不太大”。当然这个定义有点“不太数学”。

考虑到一个h层深度的满树能容纳的节点数n为：

$$n = 2^h - 1$$

因此，对于一个n个节点的树，我们能获得的最小的高度为：

$$h = \lceil log_2(n + 1) \rceil$$

我们可以把平衡树定义为：

$$h \le k * \lceil log_2(n + 1) \rceil$$

其中k可以视为平衡系数。显然当k=1时，树不可能更“平衡”了，当k是常数时，我们访问树的任意节点的时间复杂度不超过$klog_2n$，也就是$O(log_2n)$。显然我们可以认为，这个时候树是平衡的。

由于ceil函数在分析时会给我们带来麻烦，因此我们把上面的条件弱化为：

$$h \le k * log_2n + b$$

其中k和b都是常数。这个时候访问任意节点，我们的时间复杂度仍然不超过$log_2n$。

需要注意的是，上面的这些定义都是仅限于这篇文章（虽然你拿出去用问题也不大）。另外在实际设计设计过程中，不需要把这些东西精确的写出来，一般模糊的给自己一个感觉：访问节点的时间最糟情况下应该是对数时间，就够了。

前面我们已经分析了红黑树是可以满足这个条件的。而且是一棵非常好的平衡树(k=2，实际上k<2因为我们进行了一个比较“大方”的缩放，具体数值有兴趣可以自行细算)。

如果同学们有兴趣的话，还可以对AVL树进行一下分析，AVL分析的过程中还可以出现很好玩的斐波那契数列哈哈哈。然后可以得到一个k大约等于1.44（随手算的，错了请无视）。可见AVL比红黑树平衡性要更强。

当然，平衡性更强不代表数据结构更好，虽然更强的平衡可以在访问时获得更短的路径，但是更强的平衡性同时会导致插入删除过程中更多的失衡调整。因此具体那种情况更有，还需要更多的考量。当然已经超越本文探讨的范畴了。

1. 可行性分析

我们需要分析使用子树size进行平衡的可能性。这时我们首先引入我们的第一个约束：

约束1：每个节点附带一个size = 所在节点以及所有子节点的个数

这是一个蛮简单明了的约束，显然，维护这么一个约束并不难。每次插入时，我们只需要从插入位置一直到根节点，一路更新size即可。对于删除问题也差不多。

当然，这个约束明显不足以建立平衡树，我们需要考虑在这个约束的基础上再加入更复杂的约束。这时我们需要考虑几个条件：

通过某种对左右树size的约束，对于任何情况，树是可以建立起来的。

第一个条件是明显需要满足的，否则树都不能建立起来，那还平衡个毛线。这条看起来很废话，但是实际上却不能不考虑。例如假设我们引入一个约束：

$L \le 2R, R \le 2L$。（其中$L, R$分别为左右子树大小）

这个乍一眼一看是一个蛮合理的约束，但是咱考虑一下，假设一棵树有两个节点$n=2$，这棵树怎么办？

显然我们需要1个根节点，那么我们把剩下的一个节点放入到左侧时，$L \le 2R$就不成立了。反之，$R <= 2L$就不成立了。因此，上述的约束不是一个可行的约束方案。

但是考虑一下 $L \le 2R + 1, R \le 2L + 1$，树就可以建立起来了。

通过约束，可以推导出平衡特性

这显然又是一句废话，我们的目标是设计一颗平衡树，如果树不平衡我们还玩毛线啊。因此我们需要一个证明，证明只要我们的size一直符合我们的约束，树就是平衡的。

在上面的例子中，我们用的是$L \le 2R + 1, R \le 2L + 1$。但是我们在后面的研究中，系数2和1其实可能是会发生变化的，为了给后面留有余地，我们这里证明一下，如果一棵树任意节点的：$L \le kR + b, R \le kL + b$，这颗树是平衡的。其中$k \ge 1, b \ge 1$。

对于一颗树有n个节点，并满足我们上述所说的约束，那么有：

$$子树节点数 \le min\{ \frac{n - 1 - b}{k + 1} * k + b, n - 1 \}$$

为了便于描述，我们把整棵数的节点数记为$n_0$，并把第二层节点最大可能数值记为$n_1$，然后是$n_2$，$n_3$…

那么上述公式转为：

$$n_{i+1} \le min\{\frac{n_i-1-b}{k+1} * k + b, n\_i - 1\}$$

然后就是引入我们最喜欢的换元大法，另 $m_i = n_i + k - b$，上式转换为：

$$m_{i+1} = n_{i+1} + k - b \le \frac{n_i-1-b}{k+1} * k + k = m_i * \frac{k}{k+1}$$

因此：

$$m_i \le m_0{(\frac{k}{k+1})}^i$$ $$n_i \le (n_0 + k - b){(\frac{k}{k+1})}^i - k + b$$

当$n_0 + k - b \le 0$时，树的高度$h <= n_0 <= b - k$ 是一个常数。

当$n_0 + k - b > 0$时，我们希望上面式子里的指数部分<=1，因此有：

$$(n_0 + k - b){(\frac{k}{k+1})}^i <= 1$$

这时，两侧取对数，我们可以得到：

$$i \ge \frac{log_2(n_0 + k - b)}{log_2{\frac{k+1}{k}}}$$

因此我们知道：

$$h \le \frac{log_2(n_0 + k - b)}{log_2{\frac{k+1}{k}}} + max\{b - k, 0\}$$

上式中，除了log内部的部分，其他都是常数，因此当我们引入约束$L <= kR + b, R <= kL + b$时，我们可以获得一棵平衡树。

当然，有了上面两个部分还不够，我们还需要引入一个更困难的问题：

当树进行了插入/删除操作后，我们必须在最多O(log2n)次调整内，让树恢复约束

也就是说，上面两个条件虽然能够建立一棵平衡树，但是如果说我们每次插入/删除后，我们需要花费O(n)的时间去重新让树平衡，那么我们的数据结构显然也是没有意义的。

这步也是我们设计的最核心的地方，我们下面要继续讨论。

2. 树的旋转，以及计数维护

当我们讨论平衡树时，自然的我们需要去讨论树的旋转和等价。

在一般的树中，我们认为只有两棵树在结构上完全一致的，我们才认为这两棵树是等价的。显然，如果我们继续沿用这个主意的话，一棵不平衡的树我们歪脑袋也不可能给调平衡了。

因此，一般在平衡树中我们认为：如果两颗树的中序遍历是一致的，我们就认为两棵树是等价的。

OK，基于这一点，我们有了树的旋转（盗图wikipedia，点链接还可以看动态图）：

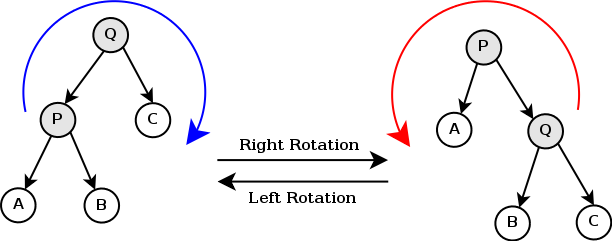
在上面的旋转过程中，A仍然在P的左侧，B仍然在P、Q中间，C仍然在Q的右侧，因此旋转后，树的中序遍历没有发生变化。

由于我们在每一个节点上附加了子树尺寸信息，因此我们需要重新调整附加的子树信息，为了叙述的更加简洁，我们后面的文章里直接用节点的字母来代表节点的size。并且用’来代表旋转后的节点尺寸，例如P’，Q’。

A，B，C以及A，B，C的所有子节点都未发生变动。

当树发生右转时，Q变为P的子节点 $Q' = B + C + 1$

变为新的根节点 $P' = A + Q' + 1$

由于树的旋转是对称的，因此我们在下面的讨论中，只需要讨论一种旋转，而另一种情况下是等价的。

3. k和b的选择

在上面的文章中，我们讨论了当树满足约束 $L \le k R + b, R \le k L + b$ 时，树为平衡树。这里我们显然要选择一对合适的k和b来继续我们的设计。

由于我们上面的证明假定了$k \ge 1$，那么我们从$k = 1$开始考虑。

首先，$k = 1$看起来不是那么的合适。当$k = 1$时，我们如果一直向尾部追加元素，每插入n个元素，我们就会导致根节点发生$\frac{n}2$次旋转，显然这个太频繁了，能不能行得通暂时不说，光效率看起来就不太合适。

从技术上来说，我们当然可以取$k$为小数，例如$k = 1.5$。但是作为一个程序员，显然的，没有人会跟自己过不去。

那么我们暂且取$k=2$。

然后我们需要考虑$b$，前面我们已经证明了$b \ge 1$，感觉$b = 1$看起来还是蛮可行的。

OK，我们暂时考虑取$k = 2, b = 1$。

那么我们有：$L \le 2 R + 1, R \le 2 L + 1$

注：后面的文章中可以看到，事实证明k=2是行不通的，囧。但是毕竟这篇文章是指导如何设计数据结构的，而不是说，这个数据结构是可以的，因此我把不可行的部分也保留下来了，以便与同学们了解整个设计过程

4. 插入时的维护

这时，我们首先考虑一种较为简单的情况，维护插入。

第一种旋转

OK，我们重新摆出从wiki盗的图：

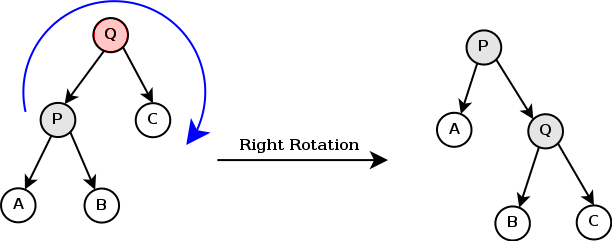
假如说我们进行了某次插入后，在Q节点发生失衡（约束冲突）。为了简化下面的讨论，我们假定插入发生在Q的左侧，如果插入发生在Q的右侧，那么只需要把下面证明中所有的部分翻转过来即可。

当插入发生在Q的左侧，并发生了冲突时，显然是发生了 $P > 2 C + 1$。由于我们每次只插入1个元素，因此可知，此时：$P = 2 C + 2$

OK，我们先试试直接向右旋转。

旋转发生后，我们发现A、B、C以及它们的所有字节点都没有发生变换。显然A、B、C以及它们的所有子节点原来满足约束，现在肯定也满足约束。

我们先来看Q节点。

$$B = P - 1 - A \le P - 1 = 2 C + 1$$ $$2 B + 1 \ge 2 \frac{P - 2}{3} + 1 = \frac43 C + 1 >= C$$

运气不错，旋转后的Q节点是平衡的。

再来看看P节点。

$$2 Q' + 1 = 2(B + C + 1) + 1 \gt 2 C + 2 = P \gt A$$

最后我们只需要再证明$2 A + 1 \ge Q'$就大功告成了。。。

很可惜，高兴的太早了。。。。上面这个是不一定成立的。。。当$A = 1, B = 3, C = 1$时，来回的转都没有用。。。。那怎么办？？？

其实观察一下上面这种情况就知道，这个问题发生的核心原因是，B节点太大了，但是旋转的时候，只能把B节点从一侧挪到另一侧，放左边时，左边太大，放右边时，右边又炸了。所以我们必须想办法给B子树拆了，否则这个问题没法解决。

damn，我们引入第二种旋转。。。

第二种旋转

首先，我们必须明确一点，如果第一种旋转已经OK了，那明显就不需要第二种旋转了。因此我们在进行第二种旋转时，有一个前提条件：$2 A + 1 < Q' = B + C + 1$，也就是 $2 A < B + C$。

Sadly，这次没地方可以盗图了，自己画吧。。。。

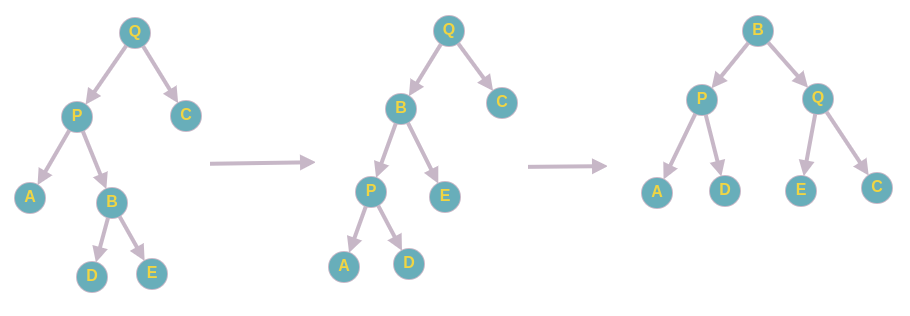
哈哈，凑合看，大家见谅。（欢迎提供好看的图，lol）

显然，第二种旋转要进行的话，我们有个前提条件，就是B节点要存在。。。

我们假设 $A \ge B$，那么有：$2A - B \ge A \ge \frac{P - 1}2 = \frac{2C + 1}2 > C$。和我们进行第二种旋转的前提条件冲突。因此我们有 $A < B$。因此$B > 0$，所以B节点必然存在。

接下来就是漫漫长征啊，我们需要证明P, Q, B节点都是符合约束的。

先看节点P：

$$2A + 1 \ge B > D$$

然后。。。。。。这里我想插入一个超diao的表情啊，，，，lol

大家会发现无论如何也证明不了 $2D + 1 \ge A$。

对的，因为这tmd的的确就是不成立的。。。。

我们另C = 1000, P = 2002, A = 1000, B = 1001, D = 333, E = 667。显然这是一组“好好”的反例啊。

这时候怎么办？有两种思路：

• 方案一：我们接着往下修P节点，但是必须证明接着往下修在有限步数内一定能给修好。
• 方案二：调整约束

在上次失败的时候，为什么我们不尝试调整约束，而是继续往下修呢？因为上次的情况调整约束是不能解决问题的。因为无论我们如何调整约束，当B过大时，通过第一种旋转永远无法解决B过大的问题。

但是这次的情况和上次有所不同。核心原因是调整系数k会影响我们这次的情况。

经过短暂的尝试后，个人放弃了往方案一方向的探索。（不等于方案一一定行不通）。

5. 调整参数k

观察到现在问题的核心是B太小，而A太大导致的。那么我们能不能尝试调整我们的参数来绕开这个问题？

通过上面的证明，我们知道第二种旋转触发时$A \le C$，因此

$$B = P - A - 1 = kC + 1 - A \ge kA + 1 - A = (k-1)A + 1$$

由于我们第一次尝试时，选择的k等于2，因此导致A和B数值上过于接近，进而导致第二类旋转不能保证约束。通过上面式子我们可以观察到，如果我们把k从2改为3，可以快速的拉开A和B的差距。

但是具体需要改多大，还需要进一步的尝试。做了一些简单的尝试后，我们把k从2改为3，拿到我们第二组常数：$k=3, b=1$

6. 再来一次（lol）

由于我们在上面的设计中，调整了约定，因此，我们现在面临着一个非常“nice”的情况。

对的，上面的所有证明都要重来一次。。。。。

实际上，在设计数据结构的时候，就是这样反复的过程。每一次约束的修改，就像是推翻重做一样。任意一个非常小的约束修改，都有可能导致新的问题。而数据结构设计，就是在夹缝之中寻找出一条小径。

实际上在我设计这个数据结构时，我还遇到了一次重新证明。也就是在处理删除数据时，我又一次重新证明来过了一遍。

本来我还想做一个冷笑话，放进去大家乐乐的，哈哈哈。考虑到我现在打字打的快呕心沥血了，也就不给自己再找罪受了。

考虑删除情况

先重新贴份图方便看的：

在我们前面的推演中，我们假定了我们是插入左侧导致了约束被破坏。由于我们每次插入时最多只插入一个元素，因此当$P > 3C + 1$，我们必然有：$P = 3C + 2$。

这次我们同时把删除的也考虑了，其实在我自己推演时，我是先推演了插入的维护，再推演删除的维护。

但是考虑到我现在手快要抽筋了，咱们还是能省则省吧。

当我们在考虑插入时，当树的左侧L插入一个元素，那么显然不可能破坏$3L + 1 \ge R$这个约束。因此只可能破坏$3R + 1 >= L$这种情况。我们将不等式稍作调整，有$L - (3R + 1) <= 0$。

当失衡发生时，有$L - (3R + 1) > 0$。这时，我们可以用$L - (3R + 1)$来衡量失衡的程度。显然，失衡程度越大，想要一次性修复的难度越大。由于每次失衡后，我们会立即进行修复。因此当发生插入失衡时，$L - (3R + 1) \le 1$。

其实当发生删除时，情况非常的类似。同样为了便于讨论，我们只讨论删除右侧的情况，也就是减少R。同样我们每次失衡后会立即进行修复，因此当发生删除失衡时，我们有$L - (3R + 1) \le 3$

回到我们图片中的符号，我们有：$3C + 1 < P \le 3C + 4$。其实这个不等式的调整，对于大部分的证明来说都是不影响的。但是还是有部分的东西让我折腾了很久。

第一种旋转

由于调整了插入元素个数的不等式，使得我们这次的证明变得繁琐了很多。首先我们继续考虑Q’下的情况。

$$3B + 1 \ge 3\frac{P-2}{4} + 1 \ge \frac94 C + 1 > C$$

但是我们证明$3C + 1 \ge B$时，我们遇到了个很大的麻烦：

$$3C + 1 \ge P - 3 \ge \frac{B-1}3 * 4 + 2 - 3 = \frac43B - \frac73$$

当上面的式子中，$B \ge 7$时，$3C + 1 \ge B$即可成立。

当然，我们可以想办法继续调整参数绕开这个问题，例如放宽b，使得b=2。但是考虑到这里B仅仅在较小的时候有例外。因此我们做个简单的穷举：

• C = 0时，B <= 2，存在一个反例
• C = 1时，B <= 4，全部满足约束
• C = 2时，B <= 7，全部满足约束
• C >= 3时，B取[0,6]满足约束，B取7以上也满足约束

综上可知，仅当C = 0，B = 2时，我们可以找到一个冲突。但这个问题不大，如果遇到这种情况时，我们再对Q’进行一次向右旋转即可解决问题。

OK，我们来继续看P’下的情况。

$$3Q' + 1 > 3B + 1 \ge A$$

最后，我们又回到了上次的场景，我们无法保证$3A + 1 \ge Q'$。为此我们分两种情况处理：当满足$3A + 1 \ge Q'$时，我们使用第一种旋转进行修正，当不满足这个情况时，我们祭出第二种旋转。

同样注意，当进行第二种旋转时，我们有：

$$3A + 1 < Q' = B + C + 1$$ $$3A < B + C$$

第二种旋转

不知道有多少人能看到这里哈，不过一个好消息是，我们的证明就要结束了。

为了方便后面的证明，我们先在这里把一些通用性的东西证明出来：

首先我们有第二种旋转的触发条件：

$$3A < B + C$$

通过这个我们可以推导出：$A \le C$，证明如下：

假设$A > C$，则有 $A \ge C + 1$，则有 $3A \ge 3C + 3 \ge P - 1 = A + B > B + C$，和上式冲突，因此有：

$$A \le C$$

由于$P > 3C + 1$，因此$A + B > 3C \ge 3A$，因此：

$$B > 2A \\ B \ge 2A + 1$$

由于$P = A + B + 1 > 3C + 1$，因此：

$$A + B > 3C \\ A + B \ge 3C + 1$$

由于$A \ge \frac{P - 2}4$，因此：

$$A \ge \frac{3C}4$$

OK，现在回到证明P’节点是满足约束的。

$$3A + 1 \ge B > D$$ $$3D + 1 \ge 3 * \frac{B-2}{4} + 1 \ge 3 * \frac{2A - 1}{4} + 1 = \frac32 A + \frac14 > A$$

然后是证明Q’节点是满足约束的。

$$3C + 1 \ge 3A + 1 \ge B > E$$ $$\begin{align} 3E + 1 &\ge 3 * \frac{B-2}4 + 1 \\ &= \frac34 B - \frac12 \\ &=\frac12 B + \frac14 B - \frac12 \\ &\ge \frac12 B + \frac14(2A + 1) - \frac12 \\ &= \frac12(A+B)-\frac14 \\ &\ge \frac12(3C + 1) - \frac14 \\ &= \frac32 C + \frac14 \\ &> C \end{align}$$

最后证明B’节点满足约束。

$$\begin{align} 3P' + 1 &= 3(A+D+1) + 1 \\ &=3A + (3D + 1) + 3 \\ &\ge \frac94 C + E + 3 \\ &\ge C + E + 3 \\ &= Q' + 2 \\ &> Q' \end{align}$$ $$\begin{align} 3Q' + 1 &= 3(E+C+1) + 1 \\ &= (3E + 1) + 3C + 3 \\ &\ge D + 3A + 3 \\ &\ge D + A + 3 \\ &= P' + 2 \\ &> P' \end{align}$$

最后我们要非常装Bility的写下：

$$Q.E.D \tag * {$\blacksquare$}$$

7. 代码实现

看完上面的乱七八糟的证明，我估计大家都已经晕了，我们新设计的数据结构到底怎么用。这里简单的汇总一下吧。

首先，我们需要在节点上附加一个整型的数字，size，并维护size为节点以及所有子节点的个数。考虑到我们写这篇文章面向的读者，这里就不再累述该如何维护size了。

然后，每当我们每次对树进行了修改之后，我们需要从修改处一直往上遍历，检测是否每个节点都满足约束left->size * 3 + 1 >= right->size && right->size * 3 + 1 >= left->size。当left或者right不存在时，我们视同为left->size或right->size等于0。

如果发现某个节点不满足约束时，我们进行如下操作：

• 当left->size > right->size时，我们将树从节点处，进行一次向右操作。
• 当left->size < right->size时，我们将树从节点处，进行一次向左操作。

其中向左和向右为对称操作，这里简单以向右操作为例。

当我们进行向右操作时，我们需要先检查是否满足left->left->size >= left->right->size + right->size，如果满足，我们进行第一种旋转，否则我们进行第二种旋转。

第一种旋转

当我们进行第一种旋转时，我们直接对节点进行向右或者向左旋转，具体旋转逻辑参见：Tree Rotation

当我们在进行向右旋转时，当我们旋转完了后，我们需要检测是否right->right->size == 0 && right->left->size == 2。如果是的话，我们需要对right再进行一次平衡，这里有可能是第一种旋转，也有可能是第二种旋转。

当我们在进行向左旋转时，情况和上面镜像处理。

经过操作后，可以保证节点进入满足约束状态，可以继续向上遍历。

注意，当进行旋转操作时，节点附加的size数据也需要进行维护。

第二种旋转

当我们进行第二种旋转时，我们需要进行两次旋转操作。这里以向右旋转为例。

我们先需要对left进行一次向左旋转，然后再对节点本身做一次向右旋转。

当我们在进行向左旋转时，情况和上面镜像处理。

经过操作后，可以保证节点进入满足约束状态，可以继续向上遍历。

同样需要注意，当进行旋转操作时，节点附加的size数据也需要进行维护。

8. Thanks to

最后再感谢一下”杀出一条蟹路“同学帮忙复核数学推理。:)