如何制作一个"好用"的音量控制滑槽
音量控制滑槽啥的,我相信对每个“经验丰富”的程序员来说都是分分钟的事情。但是我今天为啥要拿出来谈这个事情呢?因为再小的东西都有细节。而且吧,还一定会有人踩进去。
相信同学们一定一定有过这种体验:到了晚上,音量拖到最小的一格仍然太大,再往左一拖就静音了。白天吧,音量区右边的一大半都没太大区别。
线性空间/对数空间
为啥会有这样的问题:人对音量的感知的范围非常的大,通常上来说一个正常人的耳朵在 20dB - 90dB 之间的范围都处于“比较舒适”的状态,但是这个范围足足有倍。如果再算上不太舒适区域的话,上个十万倍都是轻轻松松的。
但很多人写程序的时候并没有去考虑这么多,往往直接把这么大的空间直接线性的映射到音量控制滑槽上。导致的直接结果就是:音量大的区域,拉半天也没啥变化,音量小的区域,稍微一拖就没了。
那这个问题怎么办?其实只要简单的音量进行对数化处理就好了,废话不多说,直接上代码:
#include <math.h>
static const int VOLUME_SLIDER_MIN = 1;
static const int VOLUME_SLIDER_MAX = 30;
static const float VOLUME_MIN = 0.005;
static const float VOLUME_MAX = 1;
// 将滑槽块位置换算为音量系数
float sliderPosToVolume(int pos) {
// 特殊处理,最左侧一格表示静音
if (pos < VOLUME_SLIDER_MIN)
return 0;
// 计算对数化区间,(这不是个性能很敏感的函数,所以就直接丢这里了)
float l_min = log(VOLUME_MIN);
float l_max = log(VOLUME_MAX);
// 在对数区间线性插值
float l_vol = (l_max - l_min) / (VOLUME_SLIDER_MAX - VOLUME_SLIDER_MIN) * pos + l_min;
// 把对数空间转换转换回线性空间
return exp(l_val);
}
// 将音量系数换算为滑槽位置
int volumeToSliderPos(float vol) {
// 特殊处理0值
if (vol < VOLUME_MIN)
return 0;
// 计算对数化区间和数值
float l_min = log(VOLUME_MIN);
float l_max = log(VOLUME_MAX);
float l_vol = log(vol);
// 计算滑块位置
float pos = (l_vol - l_min) / (l_max - l_min)
* (VOLUME_SLIDER_MAX - VOLUME_SLIDER_MIN) + VOLUME_SLIDER_MIN;
// 裁剪输出
if (pos > VOLUME_SLIDER_MAX)
pos = VOLUME_SLIDER_MAX;
// 四舍五入并返回
return (int)roundf(pos);
}
上面的代码其实非常的简单,我相信不需要多解释。唯一特殊注意就是0值。在对数空间里是没有0值的,但是现实世界里却是有静音的,因此需要特殊的处理。
拿对数化计算0.5的阶乘(0.5!)
其实对数化是一个非常非常好玩又好用的东西。当很多问题数值非常大或非常小或者变化区间非常大时,丢一个对数化下去经常会有惊喜。
例如很多人对n!非常的感兴趣(哈哈哈,其实说的就是我自己啦)。但是真要研究琢磨一下的,完全没法下手。只知道增长的很快很快。完全没法画图。但如果拍一个log下去:
其实对数化了之后,明显可以看出log(n!)在一个蛮大的区间里是接近线性的。是不是很有惊喜?
我们知道,那么我们是不是也可以假设呢?那么把这个反过来:
然后呢,由于在n很大的时候,log(n!)是接近线性的,OK!瞬间有思路了,来来来,我们也走一个。(js代码,不想写c自虐了,哈哈哈)
// 先写个函数计算log(n!)
function log_fact(n) {
var lf = 0;
for (var i = 1; i <= n; ++i) {
lf += Math.log(i);
}
return lf;
}
// 恩恩,取个很大n,使得空间尽可能线性
var lf_10000 = log_fact(10000);
var lf_10001 = log_fact(10001);
// 线性插值,计算log(10000.5!)的近似值
var lf_10000_5 = (lf_10000 + lf_10001) / 2;
// 一步一步减去10000.5, 9999.5, 9998.5, ....
var lf_0_5 = lf_10000_5;
for (var i = 10000; i >= 1; --i) {
lf_0_5 -= Math.log(i + 0.5);
}
// 从对数空间换算回指数空间
var fact_0_5 = Math.exp(lf_0_5);
console.log(fact_0_5);
嗯嗯,我们得到个结果0.886238002222443,看起来似乎没啥特殊的哈,我们给这个数值平方一下,再乘以4:
console.log((fact_0_5 * 2) ** 2);
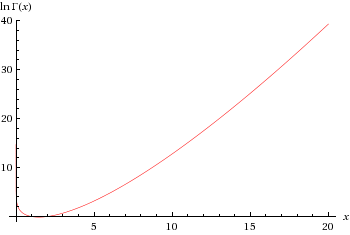
3.1416711863329074!咋样,吓一跳吧,这不就是PI么,哈哈哈哈。其实历史上第一个计算0.5!的人还真就是这么干的:就是先把n!对数化再进行拟合插值,再换算回去。下面这个图就是插值完的函数(实际上是log((n-1)!))
把我们刚刚计算0.5!的公式展开的话,又会有新的好玩的东西:
组合一下上面两条公式,我们得到:
非常不负责任的把n推向无穷大后有:
由于前面知道,所以:
哇啊啊啊啊啊,这就是传说中的“沃利斯公式”啊。哈哈哈,当然,我这里纯属瞎证明哈。其实在历史上是恰好反过来,用“沃利斯公式”证明的。
对数化处理贝叶斯分类器
再一个边写文章就边随手想到的例子就是贝叶斯分类器了,相信不少人手摞代码的时候都被前面的0给绕晕了。如果参数集再大一些,最后浮点数全0是非常正常的现象。再拍一个log下去:
大部分的时候,用贝叶斯只是为了找出最大的,连换算回去的步骤都省了。另一个好处是,log拍下去之后都可以用矩阵运算,还可以并行了,23333。再眼尖点的,还会发现对数完后的贝叶斯怎么和logistic有点像,哈哈哈哈。
哈哈哈哈,不能再说了,再说就要暴露自己几斤几两了。。。。其实我本来只不过想吐嘈一下某某播放器晚上“有点吵”而已,:’)