是否存在一个函数，它的三阶导是函数本身

“众所周之”，指数函数的求导是函数自身，而sin(x)的4阶求导（也就是求导四次的啦）是sin(x)本身，表示成数学公式就是：

$(e^x)' = e^x$ $(sin(x))^{(4)} = sin(x)$

一直很好奇，是否存在一个函数，它的二阶求导是函数本身。如果存在这么一个函数的话，是否还存在一个函数，它的三阶求导是函数本身呢？那如果推导到更广泛的n阶呢？

本来只是无聊的好奇，没想到经过一顿搜索之后，竟然找到了超乎意料的漂亮的解，相当的意外，板砖过来给大家围观。

什么函数的二阶求导是函数本身

在研究探讨三阶求导是函数本身之前，先琢磨一下一个更简单的问题是有好处的。毕竟对于问题n=1和n=4都存在的情况下，n=2存在的可能性明显是比n=3存在的可能性要高很多的。

首先，作为这个问题的趣味性，我们是肯定要先排除 $e^x$ 这个答案的。否则的话，这个问题就变得很无聊了，毕竟 $e^x$ 的导数就等于本身了，再给自己求n次导数都是自己本身。所以其实我们要找的是一个函数，使得： $f''(x) = f(x) 但 f'(x) \neq f(x)$ 。

这个其实不是那么困难，考虑一下：

$(e^{wx})' = w * e^{wx}$

再来一次：

$(e^{wx})'' = w^2 * e^{wx}$

其中， $e^{wx}$ 部分就是原本的部分，那我们把w=-1，得到：

$(e^{-x})'' = (-e^{-x})' = e^{-x}$

什么函数的三阶求导是函数本身

Cool，我们来到了我们真正感兴趣的问题了，我们先把已知的部分列一下：

$\begin{align} \text{n = 1:}\quad & e^x \\ \text{n = 2:}\quad & e^{-x} \\ \text{n = 4:}\quad & sin(x) \\ \end{align}$

其实问道到这里，线索已经非常的清晰明了了，就差大声喊出来了。但是可惜的是，我一直被sin/cos的所迷惑。如果我们把上面证明n=2的过程再哪来用一次：

$(e^{wx})^{(4)} = w^4 * e^{wx}$

$w^4 = 1$ ？？这不就是 $w = \pm1$ 么？What？等等，回忆一下高中复数课程，w还有两个解， $w = \pm{i}$ 。Bingo！我们把 $w = i$ 代进去：（当然，你要把w=-i带入进去也可以）

$\begin{align} (e^{ix})^{(4)} & = i * (e^{ix})^{(3)} \\ & = i^2 * (e^{ix})'' \\ & = i^3 * (e^{ix})' \\ & = i^4 * e^{ix} \\ & = e^{ix} \end{align}$

这个奇怪的 $e^{ix}$ 到底和 $sin(x)$ 什么关系？是时候该拿出理科生骗文科妹子专用公式（欧拉公式）了：（可惜我是工科生，23333）

$e^{ix} = cos(x) + isin(x)$

然而，我们这里并不是要欧拉公式，我们把欧拉公式变形一下：

$sin(x) = \frac{e^{ix} - e^{-ix}}{2}$

根据“最最基础的求导公式”，我们知道：

$(w * f)' = w * f',\quad (w * f)^{(n)} = w * f^{(n)}$ $(f + g)' = f' + g',\quad (f + g)^{(n)} = f^{(n)} + g^{(n)}$

So:

$sin^{(4)}(x) = (\frac{e^{ix} - e^{-ix}}{2})^{(4)} = \frac{(e^{ix})^{(4)} - (e^{-ix})^{(4)}}{2} = \frac{e^{ix} - e^{-ix}}{2} = sin(x)$

综上所知：sin(x)的四阶求导等于sin(x)证毕。

等等等等，WTF？这TM不是脱裤子放屁么？好吧好吧，前面的请无视，咱重新来：

什么函数的三阶求导是函数本身（真）

其实问题到这里，大家也都知道要怎么做了，非常的简单，答案就是：

$f(x) = e^{wx}, \quad 其中w^3=1$

我们按照”高中知识”知道，w有3个解，分别是：

$\begin{align} w_1 & = 1 \\ w_2 & = cos(\frac{2}{3}\pi) + isin(\frac{2}{3}\pi) \\ w_3 & = cos(\frac{2}{3}\pi) - isin(\frac{2}{3}\pi) \\ \end{align}$

也就是说，我们至少至少已经知道了两个函数，这两个函数的3阶导是自身：（排除 $e^x$ ）

$\begin{align} f_1(x) = e^{cos(\frac{2}{3}\pi) + isin(\frac{2}{3}\pi)} \\ f_2(x) = e^{cos(\frac{2}{3}\pi) - isin(\frac{2}{3}\pi)} \end{align}$

问题到这里貌似差不多了，但我们出发的初衷是为了找个实域上的函数啊，不是想找个复平面上的啊。这不，明显又跑题了啊。但是参考资料到这里也就到头了，但咱必须继续：

不得不说上面的 $w_2$ ， $w_3$ 写起来太累了，为了下面的证明舒服点，我们先：

$a = cos(\frac{2}{3}\pi) \\ b = sin(\frac{2}{3}\pi)$

OK，这个时候：

$\begin{align} w_2 & = a + bi \\ w_3 & = a - bi \\ f_1(x) & = e^{(a+bi)x} \\ f_2(x) & = e^{(a-bi)x} \\ \end{align}$

然后呢：

$\begin{align} f(x) & = f_1(x) + f_2(x) \\ & = e^{(a+bi)x} + e^{(a-bi)x} \\ & = e^{ax} * e^{bix} + e^{ax} * e^{-bix} \\ & = e^{ax} * (e^{bix} + e^{-bix}) \\ & = e^{ax} * (cos(bx) + isin(bx) + cos(-bx) + isin(-bx)) \\ & = e^{ax} * (2 * cos(bx)) \\ & = 2 * e^{ax} * cos(bx) \\ & = 2 * e^{cos(\frac{2}{3}\pi)x} * cos(sin(\frac{2}{3}\pi)x) \end{align}$

向上面的sin(x)和cos(x)学习一下，我们给这个函数/2，得到我们最终想要的g(x)：

$g(x) = e^{cos(\frac{2}{3}\pi)x} * cos(sin(\frac{2}{3}\pi)x)$

验证这个答案的正确性，着实不是一件容易的事情啊。生命苦短，我们还是直接祭出神器来吧： derivative-calculator.net

来来来，最后来瞅瞅我们辛辛苦苦找半天的函数长啥样的：

plot

$f(x) = e^{cos(\frac{2}{3}\pi)x} * cos(sin(\frac{2}{3}\pi)x)$

plog

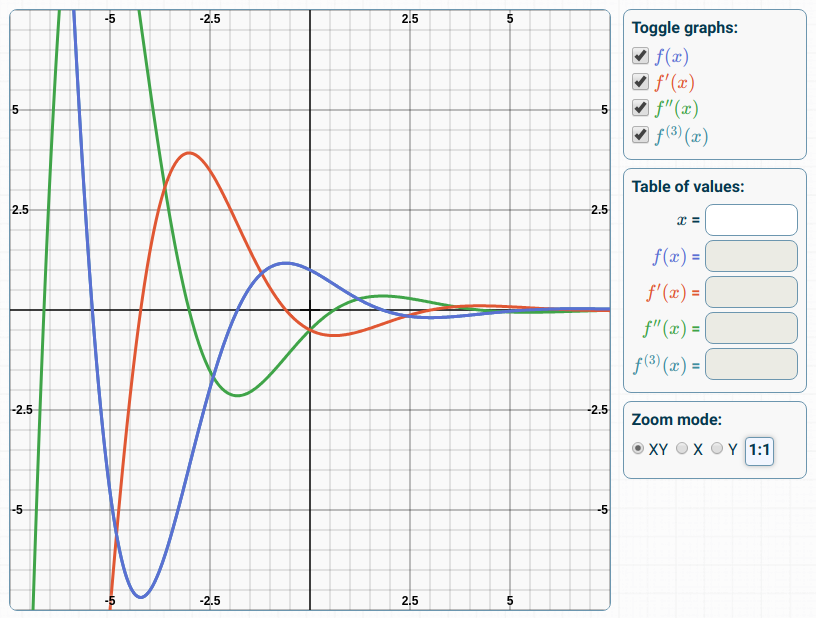
既往开来

一直以来，数学家们就是一群追（自）求（找）自（麻）我（烦）的人。找到了n=3的，自然不能止步于此，n=5呢？n=6呢？这个还真不难，至少以下函数肯定是对的：

$f(x) = e^{cos(\frac{2\pi}{n})x} * cos(sin(\frac{2\pi}{n})x)$

顺便带入一下n=1，2，4试试：

$f(x)_{n=1} = e^{cos(2\pi)x} * cos(sin(2\pi)x) = e^x * cos(0) = e^x$ $f(x)_{n=2} = e^{cos(\pi)x} * cos(sin(\pi)x) = e^{-x} * cos(0) = e^{-x}$ $f(x)_{n=4} = e^{cos({\pi \over 2})x} * cos(sin({\pi \over 2})x) = e^0 * cos(x) = cos(x)$

不错吧？哈哈。那么能不能列出所有所有的解呢？哈哈哈，貌似是可以的，但是这个着实超出本人的数学水平太多了。如果我没猜错的话，全解应该是 $e^{ {w_i}x}$ 的全部线性组合。

但其实这个问题另一个更加有趣的扩展方向是：如果我们给n=2.5会怎么样？以及给sin(x)求0.5次导会怎样？

另外一个很好玩的话题是，证明中“路过”了复数，虽然整个事情看起来和复数是没半毛钱关系的。

哈哈哈，先扯到这里，等有空了接着扯。。。